на занятия (831) 247 47 55
 eduVdom.com
eduVdom.com
Геометрия ( Справочник )
Стереометрия ( Справочник )
Математика ( Справочник )
Русский язык ( Справочник )
Физика ( Справочник )
Геометрия:
Отрезок, луч, угол
Отрезок
Луч и полуплоскость
Угол
Измерение отрезков
Измерение углов
Смежные и вертикальные углы. Перпендикулярные прямые
Треугольники
Треугольник и его элементы
Признаки равенства треугольников
Свойства равнобедренного треугольника. Третий признак равенства треугольников.
Основные геометрические построения
Окружность
Основные задачи на построение
Параллельные прямые
Определение параллельных прямых
Признаки параллельности двух прямых. Свойства параллельных прямых
Сумма углов треугольника
Теорема о сумме углов треугольника
Соотношения между сторонами и углами треугольника. Неравенство треугольника
Расстояние от точки до прямой
Признаки равенства прямоугольных треугольников
Четырехугольники
Определение четырехугольника
Параллелограмм. Расстояние между параллельными прямыми
Диагонали и признаки параллелограмма
Прямоугольник
Ромб
Квадрат
Теорема Фалеса. Средняя линия треугольника
Трапеция
Центральная и осевая симметрии
Пропорциональные отрезки
Тригонометрические функции острого угла. Теорема Пифагора
Тригонометрические функции острого угла. Определения
Теорема Пифагора
Основные тригонометрические тождества
Значения тригонометрических функций некоторых углов
Зависимости между сторонами и углами прямоугольного треугольника
Решение прямоугольных треугольников
Прямоугольные координаты
Координатная ось
Прямоугольная система координат на плоскости
Расстояние между точками
Координаты середины отрезка
Определение тригонометрических функций для любого угла от 0 до 180°
Векторы
Понятие вектора
Сложение и вычитание векторов
Умножение вектора на число
Координаты вектора
Скалярное произведение векторов
Подобие
Определение подобных треугольников
Признаки подобия треугольников
Подобие произвольных фигур
Окружность
Касательная к окружности
Центральные и вписанные углы
Вписанная и описанная окружности
Пропорциональность отрезков хорд и секущих окружности
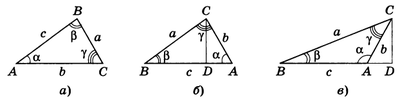
Решение треугольников
Теорема синусов и теорема косинусов
Решение треугольников
Многоугольники. Длина окружности
Ломаная
Многоугольник
Правильный многоугольник
Длина окружности
Длина дуги окружности. Радианная мера угла
Площади плоских фигур
Понятие площади
Площадь прямоугольника
Площадь параллелограмма
Площадь треугольника и ромба
Площадь трапеции
Площадь правильного многоугольника
Площадь круга и кругового сектора
Контакты









 Записаться на занятия к репетитору
Записаться на занятия к репетитору