на занятия (831) 247 47 55
 eduVdom.com
eduVdom.com
Геометрия ( Справочник )
Стереометрия ( Справочник )
Математика ( Справочник )
Русский язык ( Справочник )
Физика ( Справочник )
Математика:
Основы:
Координатная прямая, сравнение чисел
Рациональные числа
Числа и выражения:
Выражения, преобразования выражений
Степень с натуральным показателем, ее свойства
Одночлены, многочлены
Рациональные дроби и их свойства
Квадратные корни
Степень с целым показателем и ее свойства
Корень n-я степени, степень с рациональным показателем и их свойства
Тригонометрические выражения и тригонометрические формулы
Уравнения и неравенства:
Уравнения с одной переменной
Системы линейных уравнений
Квадратные уравнения
Неравенства с одной переменной и их системы
Функции и графики:
Функции, их свойства
Линейная функция (прямая пропорциональность)
Гипербола (обратная пропорциональность)
Квадратичная функция (парабола)
Степенная функция
График сложной функции
Прогрессии:
Арифметическая прогрессия
Геометрическая прогрессия
Текстовые задачи:
Решение текстовых задач
Теория вероятностей:
Теория вероятностей
Метод рационализации Нахождение множества значений функции
Действие с дробями простыми и десятичными
Формулы сокращённого умножения
Иррациональные уравнения
Контакты

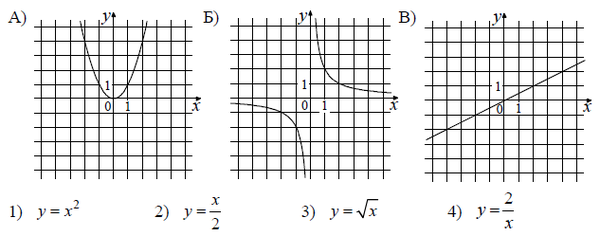







 Записаться на занятия к репетитору
Записаться на занятия к репетитору