на занятия (831) 247 47 55
 eduVdom.com
eduVdom.com
Дифференциальные уравнения (диффуры)
Теоретическая механика: статика, кинематика, динамика
Теория вероятностей и математическая статистика 
Строительная механика для строительных специальностей 
Матанализ. Дифференциальное и интегральное исчисление 
Экономика
Теоретическая механика. Статика:
Введение
Предмет механики и ее задачи
Предмет теоретической механики
Основные понятия статики
Аксиомы статики
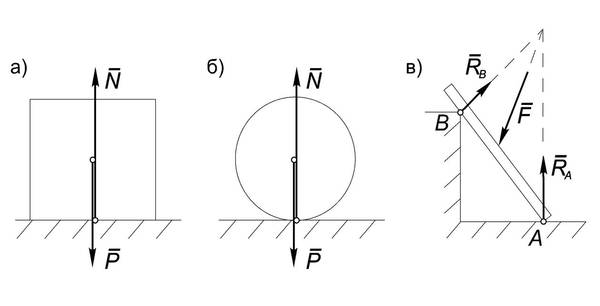
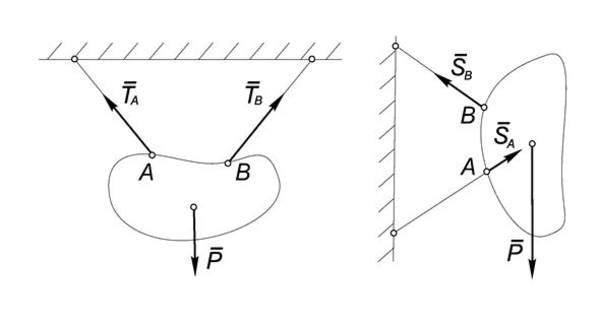
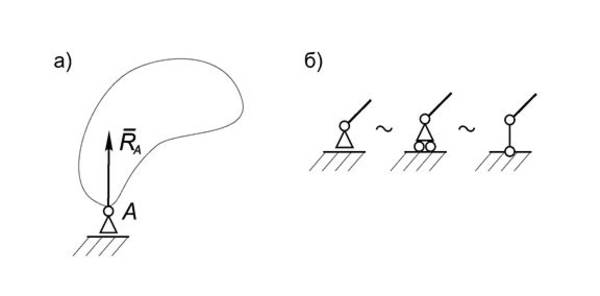
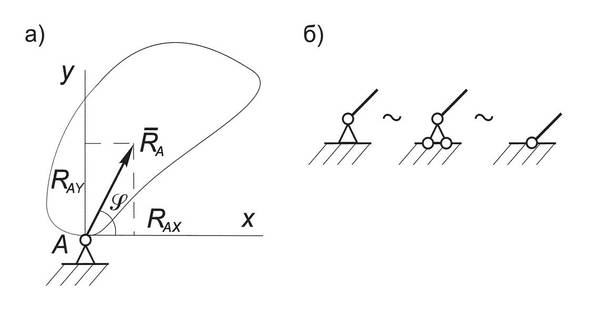
Простейшие типы связей
Система сходящихся сил
Определение и теорема о трех силах
Графическое определение равнодействующей сходящихся сил
Аналитическое задание силы
Аналитическое определение равнодействующей сходящихся сил
Условия и уравнения равновесия системы сходящихся сил
Решение задач
★ Равновесие под действием сходящейся системы сил
Теория пар сил
Момент силы относительно центра
Пара сил и ее свойства
Теоремы об эквивалентности пар
Сложение пар сил
Равновесие систем пар
Приведение плоской системы сил
Лемма Пуансо
Теорема о приведении плоской системы сил
Частные случаи приведения плоской системы сил
Уравновешенная система сил
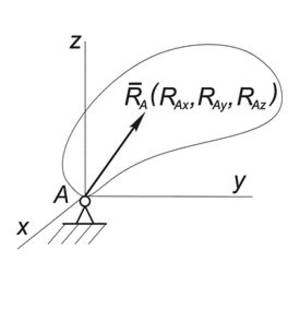
Определение опорных реакций плоских стержневых систем
★ Равновесие под действием системы параллельных сил на плоскости
Система параллельных сил
Произвольная плоская система сил
Произвольная плоская система сил. РГР 1
★ Равновесие плоской произвольной системы сил
Расчет составных систем
Расчет составных систем. РГР 2
★ Равновесие системы тел 1
★ Равновесие системы тел 2
★ Равновесие системы тел 3
Графическое определение опорных реакций
Контакты








 Записаться на занятия к репетитору
Записаться на занятия к репетитору