на занятия (831) 247 47 55
 eduVdom.com
eduVdom.com
Геометрия ( Справочник )
Стереометрия ( Справочник )
Математика ( Справочник )
Русский язык ( Справочник )
Физика ( Справочник )
Стереометрия:
Прямые и плоскости в пространстве
Параллельность прямых и плоскостей
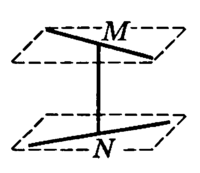
Скрещивающиеся прямые
Перпендикулярность прямых и плоскостей
Многогранники
Призма
Параллелепипед
Пирамида
Тело вращения
Цилиндр
Конус
Сфера (Шар)
Описанные шары
Вписанные шары
Контакты









 Записаться на занятия к репетитору
Записаться на занятия к репетитору