Параллелограмм. Расстояние между параллельными прямыми
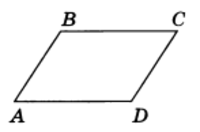
Параллелограммом называется четырехугольник, у которого противоположные стороны параллельны, т. е. лежат на параллельных прямых (рис.1).
Теорема 1. О свойстве сторон и углов параллелограмма. В параллелограмме противоположные стороны равны, противоположные углы равны и сумма углов, прилежащих к одной стороне параллелограмма, равна 180°.
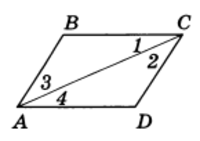
Доказательство. В данном параллелограмме ABCD проведем диагональ АС и получим два треугольника ABC и ADC (рис.2).
Эти треугольники равны, так как ∠ 1 = ∠ 4, ∠ 2 = ∠ 3 (накрест лежащие углы при параллельных прямых), а сторона АС общая. Из равенства Δ ABC = Δ ADC следует, что АВ = CD, ВС = AD, ∠ B = ∠ D. Сумма углов, прилежащих к одной стороне, например углов А и D, равна 180° как односторонних при параллельных прямых. Теорема доказана.
Замечание. Равенство противоположных сторон параллелограмма означает, что отрезки параллельных, отсекаемых параллельными, равны.
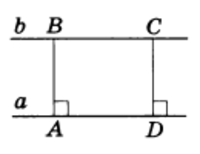
Следствие 1. Если две прямые параллельны, то все точки одной прямой находятся на одном и том же расстоянии от другой прямой.
Доказательство. В самом деле, пусть а || b (рис.3).
Проведем из каких-нибудь двух точек В и С прямой b перпендикуляры ВА и CD к прямой а. Так как АВ || CD, то фигура ABCD — параллелограмм, и следовательно, АВ = CD.
Расстоянием между двумя параллельными прямыми называется расстояние от произвольной точки одной из прямых до другой прямой.
По доказанному оно равно длине перпендикуляра, проведенного из какой-нибудь точки одной из параллельных прямых к другой прямой.
См. Диагонали и признаки параллелограмма
Пример 1. Периметр параллелограмма равен 122 см. Одна из его сторон больше другой на 25 см. Найти стороны параллелограмма.
Решение. По теореме 1 противоположные стороны параллелограмма равны. Обозначим одну сторону параллелограмма через х, другую через у. Тогда по условию $$\left\{\begin{matrix} 2x + 2y = 122 \\x - y = 25 \end{matrix}\right.$$ Решая эту систему, получим х = 43, у = 18. Таким образом, стороны параллелограмма равны 18, 43, 18 и 43 см.
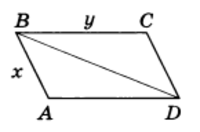
Пример 2. Четырехугольник ABCD — параллелограмм с периметром 10 см. Найти диагональ BD, зная, что периметр треугольника ABD равен 8 см.
Решение. Пусть условию задачи отвечает рисунок 4.
Обозначим АВ через х, а ВС через у. По условию периметр параллелограмма равен 10 см, т. е. 2(x + у) = 10, или х + у = 5. Периметр треугольника ABD равен 8 см. А так как АВ + AD = х + у = 5 то BD = 8 - 5 = 3 . Итак, BD = 3 см.
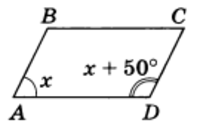
Пример 3. Найти углы параллелограмма, зная, что один из них больше другого на 50°.
Решение. Пусть условию задачи отвечает рисунок 5.
Обозначим градусную меру угла А через х. Тогда градусная мера угла D равна х + 50°.
Углы BAD и ADC внутренние односторонние при параллельных прямых АВ и DC и секущей AD. Тогда сумма этих названных углов составит 180°, т. е.
х + х + 50° = 180°, или х = 65°. Таким образом, ∠ A = ∠ C = 65°, a ∠ B = ∠ D = 115°.
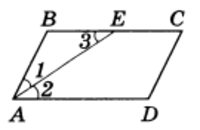
Пример 4. Стороны параллелограмма равны 4,5 дм и 1,2 дм. Из вершины острого угла проведена биссектриса. На какие части делит она большую сторону параллелограмма?
Решение. Пусть условию задачи отвечает рисунок 6.
АЕ — биссектриса острого угла параллелограмма. Следовательно, ∠ 1 = ∠ 2.
ВС || AD, АЕ — секущая, следовательно, ∠ 2 = ∠ 3, т. е. ∠ 1 = ∠ 3. А это означает, что треугольник ABE равнобедренный, следовательно, АВ = ВЕ = 1,2 дм.
ЕС = ВС - BE = 3,3 дм.
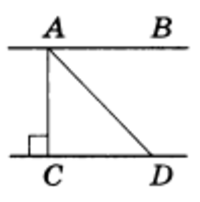
Пример 5. Прямая АВ параллельна прямой CD (рис.7).
Найти расстояние между этими прямыми, если ∠ ADC = 45°, CD = 1,6 см.
Решение. Искомое расстояние равно длине перпендикуляра АС. Треугольник ACD — прямоугольный и равнобедренный (АС — перпендикуляр), ∠ ADC = 45° по условию, значит, и ∠ CAD = 45°, ибо в прямоугольном треугольнике сумма острых углов равна 90°. Следовательно, АС = CD = 1,6 см.