Теорема Фалеса. Средняя линия треугольника

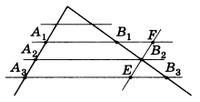
Теорема 1. Теорема Фалеса1). Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.

Доказательство. Пусть А₁, А₂, А₃ — точки пересечения параллельных прямых с одной из сторон угла и А₂ лежит между А₁ и А₃ (рис.1).

Рис.1

Пусть B₁ В₂, В₃ — соответствующие точки пересечения этих прямых с другой стороной угла. Докажем, что если А₁А₂ = A₂A₃, то В₁В₂ = В₂В₃.

Проведем через точку В₂ прямую EF, параллельную прямой А₁А₃. По свойству параллелограмма А₁А₂ = FB₂ , A₂A₃ = B₂E .

И так как А₁А₂ = A₂A₃, то FB₂ = В₂Е.

Треугольники B₂B₁F и В₂В₃Е равны по второму признаку. У них B₂F = В₂Е по доказанному. Углы при вершине В₂ равны как вертикальные, а углы B₂FB₁ и B₂EB₃ равны как внутренние накрест лежащие при параллельных А₁В₁ и A₃B₃ и секущей EF. Из равенства треугольников следует равенство сторон: В₁В₂ = В₂В₃ . Теорема доказана.

С использованием теоремы Фалеса устанавливается следующая теорема.

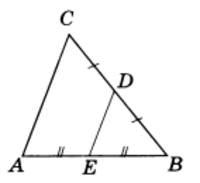
Теорема 2. Средняя линия треугольника параллельна третьей стороне и равна ее половине.

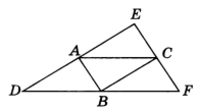
Средней линией треугольника называется отрезок, соединяющий середины двух его сторон. На рисунке 2 отрезок ED — средняя линия треугольника ABC.

ED — средняя линия треугольника ABC

Рис.2

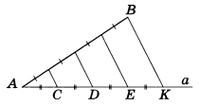
Пример 1. Разделить данный отрезок на четыре равные части.

Решение. Пусть АВ — данный отрезок (рис.3), который надо разделить на 4 равные части.

Деление отрезка на четыре равные части

Рис.3

Для этого через точку А проведем произвольную полупрямую а и отложим на ней последовательно четыре равных между собой отрезка AC, CD, DE, ЕК.

Соединим точки В и К отрезком. Проведем через оставшиеся точки С, D, Е прямые, параллельные прямой ВК, так, чтобы они пересекли отрезок АВ.

Согласно теореме Фалеса отрезок АВ разделится на четыре равные части.

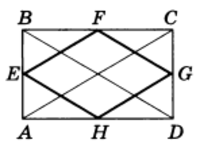
Пример 2. Диагональ прямоугольника равна а. Чему равен периметр четырехугольника, вершины которого являются серединами сторон прямоугольника?

Решение. Пусть условию задачи отвечает рисунок 4.

Рис.4

Тогда EF — средняя линия треугольника ABC и, значит, по теореме 2. $$ EF = \frac{1}{2}AC = \frac{a}{2} $$

Аналогично $$ HG = \frac{1}{2}AC = \frac{a}{2} , EH = \frac{1}{2}BD = \frac{a}{2} , FG = \frac{1}{2}BD = \frac{a}{2} $$ и, следовательно, периметр четырехугольника EFGH равен 2a.

Пример 3. Стороны треугольника равны 2 см, 3 см и 4 см, а вершины его — середины сторон другого треугольника. Найти периметр большого треугольника.

Решение. Пусть условию задачи отвечает рисунок 5.

Рис.5

Отрезки АВ, ВС, АС — средние линии треугольника DEF. Следовательно, согласно теореме 2 $$ AB = \frac{1}{2}EF\ \ ,\ \ BC = \frac{1}{2}DE\ \ ,\ \ AC = \frac{1}{2}DF $$ или $$ 2 = \frac{1}{2}EF\ \ ,\ \ 3 = \frac{1}{2}DE\ \ ,\ \ 4 = \frac{1}{2}DF $$ откуда $$ EF = 4\ \ ,\ \ DE = 6\ \ ,\ \ DF = 8 $$ и, значит, периметр треугольника DEF равен 18 см.

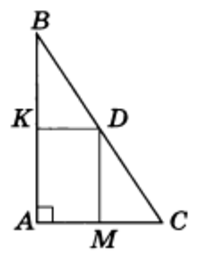
Пример 4. В прямоугольном треугольнике через середину его гипотенузы проведены прямые, параллельные его катетам. Найти периметр образовавшегося прямоугольника, если катеты треугольника равны 10 см и 8 см.

Решение. В треугольнике ABC (рис.6)

Рис.6

∠ А прямой, АВ = 10 см, АС = 8 см, KD и MD — средние линии треугольника ABC, откуда $$ KD = \frac{1}{2}AC = 4 см. \\ MD = \frac{1}{2}AB = 5 см. $$ Периметр прямоугольника К DMА равен 18 см.