Площадь параллелограмма
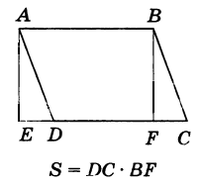
Теорема 1. Площадь параллелограмма равна произведению основания на высоту.
Доказательство. Опустим перпендикуляры АЕ и BF из вершин А и В параллелограмма ABCD (рис.1) на прямую CD.
Тогда площадь трапеции АВСЕ с одной стороны равна сумме площадей параллелограмма ABCD и треугольника ADE, а с другой — сумме площадей прямоугольника ABFE и треугольника BCF. Но так как эти треугольники равны (значит, имеют равные площади), то площадь S параллелограмма ABCD равна площади прямоугольника ABFE, т.е. S = AB•BF , или S = DC•BF ю
Пример 1. Основание параллелограмма равно 35 см, а боковая сторона — 20 см. Найти площадь параллелограмма, если боковая сторона образует с высотой, опущенной на основание, угол в 60°.
Решение. Пусть условию задачи отвечает рисунок 1.
Тогда ∠ BCF = 90° - 60° = 30° и, значит, катет BF = ½ ВС = 20 • ½ = 10 (см) (пример 3). Следовательно, искомая площадь S = 35 • 10 = 350 (см2).
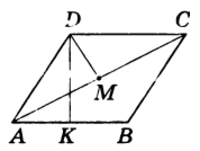
Пример 2. Дан параллелограмм ABCD со стороной АВ = 12 см и диагональю АС = 16 см. Вершина D удалена от диагонали АС на 4 см. Вычислить расстояние от точки D до прямой АВ.
Решение. $$ S_{ABCD} = 2S_{\triangle ADC} = AC•DM = 64 \text{ см}^2 \text{ (рис.1),} \\ \text{а так как }S_{ABCD} = АВ•DK\text{ , то }DK = \frac{64}{12}\text{ , т.е. }DK \approx 5,33\text{ см.} $$
Пример 3. Две стороны параллелограмма равны 10 и 9. Из одной вершины на две стороны опустили высоты, как показано на рисунке. Длина большей из высот равна 6. Найдите длину другой высоты.
Видео-решение.
| ← Площадь прямоугольника | Геометрия ( Справочник ) | Площадь треугольника и ромба → |
|---|---|---|
| Рекомендуем для обучения: | ||
| Две стороны параллелограмма... | YouTube | |