Сложение и вычитание векторов

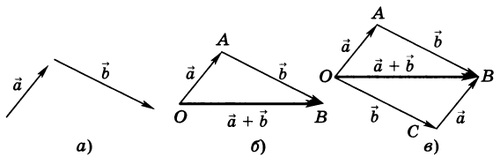
Пусть $\overrightarrow{a}$ и $\overrightarrow{b}$ — два вектора (рис.1, а).

Возьмем произвольную точку О и построим вектор $\overrightarrow{ОА} = \overrightarrow{a}$ . Затем от точки А отложим вектор $\overrightarrow{AB} = \overrightarrow{b}$. Вектор $\overrightarrow{OB}$, соединяющий начало первого слагаемого вектора с концом второго (рис.1, б), называется суммой этих векторов и обозначается $\overrightarrow{a} + \overrightarrow{b}$$ (правило треугольника).

Ту же самую сумму векторов можно получить иным способом. Отложим от точки О векторы $\overrightarrow{ОА} = \overrightarrow{a} \,и\, \overrightarrow{ОС} = \overrightarrow{b} $ (рис.1, в). Построим на этих векторах как на сторонах параллелограмм ОABC. Вектор $\overrightarrow{ОВ}$, служащий диагональю этого параллелограмма, проведенной из вершины О, является, очевидно, суммой векторов $\overrightarrow{a} + \overrightarrow{b}$ {правило параллелограмма). Из рисунка 1, в непосредственно следует, что сумма двух векторов обладает переместительным свойством: $\overrightarrow{a} + \overrightarrow{b} = \overrightarrow{b} + \overrightarrow{a}$

Действительно, каждый из векторов $\overrightarrow{a} + \overrightarrow{b} \,и\, = \overrightarrow{b} + \overrightarrow{a}$ равен одному и тому же вектору $\overrightarrow{OB}$ .

---

---

Пример 1. В треугольнике ABC АВ = 3, ВС = 4, ∠ В = 90°. Найти: $а)\,\ \overrightarrow{|АВ|} + \overrightarrow{|ВС|};\,\,\ б)\,\ |\overrightarrow{АВ} + \overrightarrow{ВС}|$ .

Решение

а) Имеем: $|\overrightarrow{АВ}| = АВ,\,\,\ |\overrightarrow{ВС}| = ВС$ и, значит, $|\overrightarrow{АВ}| + |\overrightarrow{BC}| = 7$ .

б) Так как $\overrightarrow{AB} + \overrightarrow{ВС} = \overrightarrow{АС} \,\,,\,\, то\,\, |\overrightarrow{АВ} + \overrightarrow{ВС}| = |\overrightarrow{АС}| = АС$ .

Теперь, применяя теорему Пифагора, находим $$ AC = \sqrt{AB^2 + BC^2} = \sqrt{9 + 16} = 5 \\ т.е.\, |\overrightarrow{АВ} + \overrightarrow{ВС}| = 5. $$

Понятие суммы векторов можно обобщить на случай любого конечного числа слагаемых векторов.

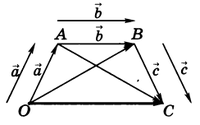
Пусть, например, даны три вектора $\overrightarrow{a}, \overrightarrow{b} \,и\, \overrightarrow{c}$ (рис.2).

Построив сначала сумму векторов $\overrightarrow{a} + \overrightarrow{b}$ , а затем прибавив к этой сумме вектор $\overrightarrow{c}$, получим вектор $(\overrightarrow{a} + \overrightarrow{b}) + \overrightarrow{c}$ . На рисунке 2 $$ \overrightarrow{ОА} = \overrightarrow{a}\,; \overrightarrow{АВ} = b\,; \overrightarrow{ОВ} = \overrightarrow{a} + \overrightarrow{b}\,; \overrightarrow{BC} = \overrightarrow{c} \\ и \\ \overrightarrow{ОС} = \overrightarrow{ОВ} + \overrightarrow{ВС} = (\overrightarrow{a} + \overrightarrow{b}) + \overrightarrow{c} $$ Из рисунка 2 видно, что тот же вектор $\overrightarrow{ОС}$ мы получим, если к вектору $\overrightarrow{ОА} = \overrightarrow{a}$ прибавим вектор $\overrightarrow{АВ} = \overrightarrow{b} + \overrightarrow{c}$ . Таким образом, $(\overrightarrow{a} + \overrightarrow{b}) + \overrightarrow{c} = \overrightarrow{a} + (\overrightarrow{b} + \overrightarrow{c})$ , т. е. сумма векторов обладает сочетательным свойством. Поэтому сумму трех векторов $\overrightarrow{a}\,,\,\overrightarrow{b}\,,\,\overrightarrow{c}$ записывают просто $\overrightarrow{a} + \overrightarrow{b} + \overrightarrow{c}$ .

Разностью двух векторов $\overrightarrow{a} \,и\, \overrightarrow{b}$ называется третий вектор $\overrightarrow{c} = \overrightarrow{a} - \overrightarrow{b}$ , сумма которого с вычитаемым вектором $\overrightarrow{b}$ дает вектор $\overrightarrow{a}$. Таким образом, если $\overrightarrow{c} = \overrightarrow{a} - \overrightarrow{b}\,,\, то\, \overrightarrow{c} + \overrightarrow{b} = \overrightarrow{a}$ .

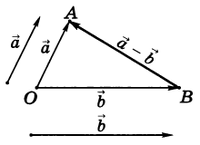
Из определения суммы двух векторов вытекает правило построения вектора-разности (рис.3).

Откладываем векторы $\overrightarrow{ОА} = \overrightarrow{a} \,и\, \overrightarrow{OB} = \overrightarrow{b}$ из общей точки О. Вектор $\overrightarrow{BA}$ , соединяющий концы уменьшаемого вектора $\overrightarrow{a}$ и вычитаемого вектора $\overrightarrow{b}$ и направленный от вычитаемого к уменьшаемому, является разностью $\overrightarrow{c} = \overrightarrow{a} - \overrightarrow{b}$ . Действительно, по правилу сложения векторов $\overrightarrow{ОВ} + \overrightarrow{ВА} = \overrightarrow{ОА} \text{ , или } \overrightarrow{b} + \overrightarrow{c} = \overrightarrow{a}$ .

---

Пример 2. Сторона равностороннего треугольника ABC равна а. Найти: $а) |\overrightarrow{ВА} - \overrightarrow{ВС}|\,;\,\ б)\,\,\ |\overrightarrow{АВ} - \overrightarrow{АС}|$ .

Решение а) Так как $\overrightarrow{ВА} - \overrightarrow{ВС} = \overrightarrow{СА}\text{ , а }|\overrightarrow{СА}| = а\text{ , то }|\overrightarrow{ВА} - \overrightarrow{ВС}| = а$ .

б) Так как $\overrightarrow{АВ} - \overrightarrow{АС} = \overrightarrow{СВ}\text{ , а }|\overrightarrow{СВ}| = а\text{ , то }|\overrightarrow{АВ} - \overrightarrow{АС}| = а$ .

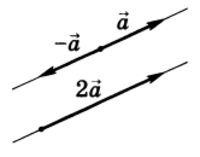
Произведением вектора $\overrightarrow{a}$(обозначается $=\lambda\overrightarrow{a}$ или $\overrightarrow{a}\lambda$) на действительное число $\lambda$ называется вектор $\overrightarrow{b}$, коллинеарный вектору $\overrightarrow{a}$, имеющий длину, равную $|\lambda||\overrightarrow{a}|$, и то же направление, что и вектор $\overrightarrow{a}$, если $\lambda > 0$ , и направление, противоположное направлению вектора $\overrightarrow{a}$, если $\lambda < 0$ . Так, например, $2\overrightarrow{a}$ есть вектор, имеющий то же направление, что и вектор $\overrightarrow{a}$ , а длину, вдвое большую, чем вектор $\overrightarrow{a}$ (рис.4).

В случае, когда $\lambda = 0$ или $\overrightarrow{a} = 0$ , произведение $\lambda\overrightarrow{a}$ представляет собой нулевой вектор. Противоположный вектор $-\overrightarrow{a}$ можно рассматривать как результат умножения вектора $\overrightarrow{a}$ на $\lambda = -1$ (см. рис.4): $$ -\overrightarrow{a} = \ (-1)\overrightarrow{a} $$ Очевидно, что $\overrightarrow{a} + (-\overrightarrow{a}) = \overrightarrow{0}$ .

---

Пример 3. Доказать, что если О, А, В и С — произвольные точки, то $\overrightarrow{ОА} + \overrightarrow{АВ} + \overrightarrow{ВС} + \overrightarrow{СО} = 0$ .

Решение. Сумма векторов $\overrightarrow{ОА} + \overrightarrow{АВ} + \overrightarrow{СВ} = \overrightarrow{ОС}$ , вектор $\overrightarrow{CO}$ — противоположный вектору $\overrightarrow{ОС}$ . Поэтому $\overrightarrow{ОС} + \overrightarrow{СО} = \overrightarrow{0}$ .

Пусть дан вектор $\overrightarrow{a}$. Рассмотрим единичный вектор $\overrightarrow{a_0}$ , коллинеарный вектору $\overrightarrow{a}$ и одинаково с ним направленный. Из определения умножения вектора на число следует, что $$ \overrightarrow{a} = |\overrightarrow{a}|\,\ \overrightarrow{a_0} $$ , т.е. каждый вектор равен произведению его модуля на единичный вектор того же направления. Далее из того же определения следует, что если $\overrightarrow{b} = \lambda\overrightarrow{a}$ , где $\overrightarrow{a}$ — ненулевой вектор, то векторы $\overrightarrow{a} \,и\, \overrightarrow{b}$ коллинеарны. Очевидно, что и обратно, из коллинеарности векторов $\overrightarrow{a} \,и\, \overrightarrow{b}$ следует, что $\overrightarrow{b} = \lambda\overrightarrow{a}$.

Таким образом, получаем следующую теорему.

---

Пример 4. Длина вектора AB равна 3, длина вектора AC равна 5. Косинус угла между этими векторами равен 1/15. Найдите длину вектора AB + AC.

Видео-решение.

---

---