Площадь круга и кругового сектора
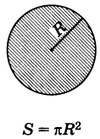
Кругом называется фигура, состоящая из всех точек плоскости, расстояние от которых до данной точки не больше данного (рис.1).
Эта точка называется центром круга, а данное расстояние — радиусом круга. Границей круга является окружность с тем же центром и радиусом.
Из наглядных соображений будем считать, что площадь круга сколь угодно мало отличается от площади вписанного в нее выпуклого многоугольника с достаточно малыми сторонами.
Пусть R — радиус круга, а C — длина его окружности. Впишем в окружность правильный n-угольник с достаточно большим числом сторон n. Площадь этого n-угольника $$ S_n = \frac{1}{2}Pr $$ , где P — периметр n-угольника, а r — радиус вписанной в него окружности (теорема 1). При возрастании числа его сторон n периметр P сколь угодно мало отличается от числа C, а радиус r — от числа R. Говорят, что при возрастании n периметр P стремится к длине окружности, а площадь $S_n$ — к площади круга S. Поэтому $$ S = \frac{1}{2}C\bullet R = \frac{1}{2} \bullet 2\pi R \bullet R = \pi R^2 $$ Итак, площадь круга вычисляется по формуле $$ S = \pi R^2 $$ , где R — радиус круга.
Пример 1. Найти площадь круга, если длина окружности равна k.
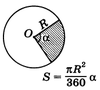
Решение. Длина окружности находится по формуле $C = 2\pi R$. Так как $C = k$ , то $k = 2 \pi R$ , или $R = \frac{k}{2\pi}$ , и, значит, площадь круга: $$ S = \pi R^2 = \pi \left ( \frac{k}{2\pi} \right )^2 = \frac{\pi k^2}{4\pi^2} = \frac{k^2}{4\pi} $$ Круговым сектором называется часть круга, лежащая внутри соответствующего центрального угла (рис.2).
Площадь сектора, дуга которого содержит один градус, равна $\frac{1}{360}$ площади круга. Поэтому площадь сектора, дуга которого содержит $\alpha$ градусов, равна $ \frac{\pi R^2}{360} \alpha $ . Итак, площадь кругового сектора вычисляется по формуле $$ S = \frac{\pi R^2}{360} \alpha \,\,\, (1)$$ , где R — радиус круга, $\alpha$ — градусная мера соответствующего центрального угла.
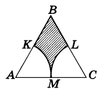
Пример 2. В равностороннем треугольнике ABC со стороной a (рис.3) дуги КМ и LM — дуги окружностей радиусов $\frac{a}{2}$.
Найти площадь заштрихованной части треугольника ABC.
Решение. Площадь треугольника ABC равна $\frac{\sqrt{3}}{4}a^2$ (пример 2), площадь каждого из секторов АКМ и CML согласно формуле (2) равна $$ \frac{ \pi\left ( \frac{a}{2} \right )^2 \bullet 60 }{360} = \frac{\pi a^2}{24} $$ Поэтому искомая площадь $$ S = \frac{\sqrt{3}}{4}a^2 - 2\bullet \frac{\pi a^2}{24} = \frac{a^2}{4} \left ( \sqrt{3} - \frac{\pi}{3} \right ) \approx 0,17 a^2 $$