Квадрат
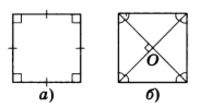
Квадратом называется прямоугольник, все стороны которого равны (рис.1, а).
Квадрат является ромбом, поэтому обладает свойствами прямоугольника и ромба. Основные свойства квадрата следующие.
Свойство 1. Все углы квадрата прямые (см. рис.1, а).
Свойство 2. Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят его углы пополам (рис.1, б).
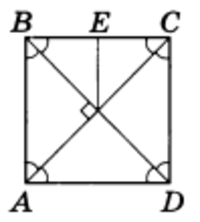
Пример 1. В квадрате ABCD (рис.2) расстояние от точки пересечения диагоналей до одной из сторон равно 1 дм. Определить периметр квадрата.
Решение. В силу основных свойств квадрата треугольник ВОС — прямоугольный и равнобедренный. Отсюда и из того, что по условию ОЕ — перпендикуляр, следует, что треугольники ВЕО и СЕО — прямоугольные, равнобедренные и равные.
Значит, ОЕ = BE = 1/2 * BC , откуда ВС = 2ОЕ и, значит, ВС = 2 дм.
Следовательно, периметр квадрата равен 8 дм.
| ← Ромб | Геометрия ( Справочник ) | Теорема Фалеса. Средняя линия треугольника → |
|---|---|---|
| Рекомендуем для обучения: | ||
| Свойства равнобедренного треугольника | ||