Теорема синусов и теорема косинусов

Теорема 1. Теорема синусов. Стороны треугольника пропорциональны синусам противолежащих углов.

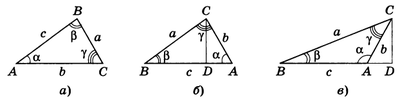
Доказательство. Пусть ABC — треугольник со сторонами $a, b, c$ и противолежащими углами $\alpha, \beta, \gamma$ (рис.1, а).

Докажем, что $$ \frac{a}{\sin \alpha} = \frac{b}{\sin \beta} = \frac{c}{\sin \gamma} $$ Опустим из вершины С высоту CD. Из прямоугольного треугольника ACD, если угол $\alpha$ острый, получаем: $CD = b \sin \alpha$ (рис.1, б). Если угол $\alpha$ тупой, то $CD = b \sin(180° - \alpha ) = b \sin \alpha$ (рис.1, в). Так же из треугольника BCD получаем: $CD = a \sin \beta$ . Итак, $a \sin \beta = b \sin \alpha$ . Отсюда $$ \frac{a}{\sin \alpha} = \frac{b}{\sin \beta} $$ Аналогично доказывается равенство $$ \frac{b}{\sin \beta} = \frac{c}{\sin \gamma} $$ Для доказательства надо провести высоту треугольника из вершины А. Теорема доказана.

Следствие 1. $$ \frac{a}{\sin \alpha} = \frac{b}{\sin \beta} = \frac{c}{\sin \gamma} = 2R $$ , где R — радиус окружности, описанной около треугольника ABC.

Справедлива и следующая теорема.

Теорема 2. Теорема косинусов. Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.
Например, $$ a^2 = b^2 + c^2 - 2bc \bullet \cos \alpha $$

---

---

Пример 1. В треугольнике ABC угол $\alpha$ равен 30°, угол $\beta$ равен 30°. Найти отношение а:с.

Решение. По теореме синусов $$ \frac{a}{\sin \alpha} = \frac{c}{\sin \gamma} $$ Используя теорему о сумме внутренних углов треугольника, имеем $$ \gamma = 180° - (30° + 30°) = 120° $$ Так как $$ sin 120° = sin(180° - 60°) = sin 60° = \frac{\sqrt{3}}{2} $$ $$\text{ , то } \frac{a}{ \frac{1}{2} } = \frac{c}{ \frac{ \sqrt{3} }{2} } \text{ , или } a:с = 1:\sqrt{3} $$

---

Пример 2. В треугольнике две стороны 20 м и 21 м, а синус острого угла а между ними равен 0,6. Найти третью сторону а.

Решение. Угол $\alpha$ острый, следовательно, $\cos \alpha > 0$ . Найдем его, используя тождество $\sin^2 \alpha + \cos^2 \alpha = 1$ : $$ \cos \alpha = \sqrt{1 - \sin^2 \alpha } = \sqrt{1 - 0,36} = 0,8 $$ Теперь по теореме косинусов имеем: $$ a^2 = 20^2 + 21^2 - 2•20•21•0,8 = 169 $$ откуда а = 13 м.

---

Пример 3. Доказать, что сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.

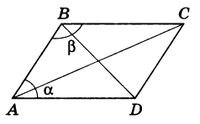
Доказательство. Пусть ABCD — параллелограмм (рис.2).

Применим теорему косинусов к треугольникам ABC и ABD. Получим $$ АС^2 = АВ^2 + ВС^2 - 2АВ • ВС • cos \beta \\ BD^2 = АВ^2 + AD^2 - 2АВ • AD • cos \alpha $$ Так как $\beta = 180° - \alpha$ , то, складывая эти равенства и замечая, что $\cos \beta = \cos (180° - \alpha) = -\cos \alpha \,; АВ = CD\,; ВС = AD$ , получим $$ АС^2 + BD^2 = АВ^2 + ВС^2 + CD^2 + AD^2 $$

---

Пример 4. Длина вектора AB равна 3, длина вектора AC равна 5. Косинус угла между этими векторами равен 1/15. Найдите длину вектора AB + AC.

Видео-решение.

---

---