Сфера (Шар)
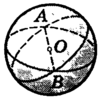
Шар – это тело, полученное вращением полукруга вокруг диаметра. Поверхность шара называется сферой. Сферу можно рассматривать как тело, полученное вращением полуокружности около её диаметра.
Сфера (Шар) является телом вращения.
Сравните:
Сфера (сферическая или шаровая поверхность) — называется геометрическое место точек пространства, равноудаленных от одной точки — центра сферы.
Тело, ограниченное шаровой (сферической) поверхностью, называется шаром. Шар можно получить, вращая полукруг (или круг) около его диаметра.
Шаром называется тело, состоящее из всех точек пространства, находящихся на расстоянии, не большем данного (радиуса шара), от данной точки (центра шара).
Центр, диаметр и радиус шара соответствует центру, диаметру и радиусу сферы.
Площадь сферы радиуса R вычисляется по формуле: $$S=4\pi\cdot R^2$$ и равна учетверенной площади большого круга.
Объем шара радиуса R вычисляется по формуле: $$V=\frac{4}{3}\pi\cdot R^3$$ и равен объему пирамиды, основание которой имеет ту же площадь, что и поверхность шара, а высота есть радиус шара.
Объем шара в полтора раза меньше объема описанного вокруг него цилиндра, а площадь поверхности шара — в полтора раза меньше площади полной поверхности того же цилиндра (теорема Архимеда).
$$ S=\frac{2}{3}\cdot S_1
\\ V =\frac{2}{3}\cdot V_1
$$
, где S1 – площадь полной поверхности, V1 – объем цилиндра.
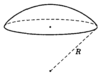
См.Рис.2.
Шаровой сегмент – это часть шара, ограниченная секущей плоскостью. Имеют место формулы: $$ V=\pi h^2 (R-\frac{1}{3}h) \\ S=2\pi\cdot Rh $$ , где V – объем шарового сегмента, S – площадь его поверхности, R – радиус шара, h – высота сегмента. См.Рис.3.
| ← Конус | Стереометрия ( Справочник ) | Описанные шары → |
| Рекомендуем для обучения: | ||
|---|---|---|
| Геометрия ( Справочник ) | ||