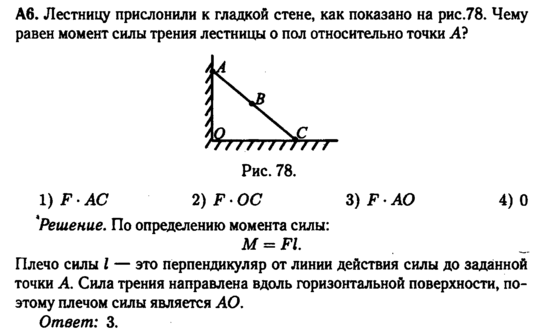
Содержание
Уравнения равновесия
Проекция силы на ось - характеризует действие этой силы вдоль этой оси.
То есть Проекция силы на ось Ох ($ P_x = \sum X_i $ ) характеризует действие этой силы вдоль оси Ох.
А проекция силы на ось Оу ($ P_y = \sum Y_i $ ) характеризует действие этой силы вдоль оси Оу.
И если сумма проекций всех сил на ось Ох равна нулю ($ \sum X_i = 0 $ )– значит действие этих сил вдоль этой оси Ох нет , силы вдоль этой оси друг друга уравновешивают.
И если сумма проекций всех сил на ось Оу равна нулю ($ \sum Y_i = 0 $ )- значит действие этих сил вдоль этой оси Оу нет , силы друг друга вдоль этой оси Оу уравновешивают.
Вращательное действие силы относительно точки О характеризует момент этой силы относительно этой точки О ($ M_0(P)=0 $) .
И если сумма моментов всех сил относительно точки О равно нулю ($ \sum M_O =0 $), то вращательного действия всех этих сил на тело относительно точки О нет, они его не производят, или их вращательные действия их взаимно уравновешены.
Теперь - если проекции всех сил на оси Ох и Оу равны нулю , и сумма моментов всех сил относительно любой - какой угодно - точки равны нулю, то тело находится в равновесии.
$$ \sum X=0 \\ \sum Y=0 \\ \sum M_A=0 $$
Это и есть условия равновесия тела под действием произвольной плоской системы тел:
Система сил, действующих на тело, называется сходящейся, если линии действия этих сил пересекается в одной точке.
Условие равновесия системы сходящихся сил
Для того, чтобы система сходящихся сил была уравновешенной, то есть под действием ее тело будет находится в равновесии -
условие равновесия системы сходящихся сил,
может быть записано :
$$ \sum X_i = 0
\\ \sum Y_i = 0
$$
Или другими словами - для плоской системы сходящихся сил, лежащих в плоскости Oxy, соответствующие уравнения равновесия примут вид:
$$ \sum X_i = 0 \\ \sum Y_i = 0 $$
Проекция силы на ось
Определение. Проекцией силы $\vec{Р}$ на ось Ox называется взятая с знаком $\pm$
длина отрезка этой оси, заключенная между проекциями на неё начала и конца
вектора силы.
Эту проекцию обычно обозначают как Рx или X. В соответствии с определением она равна:
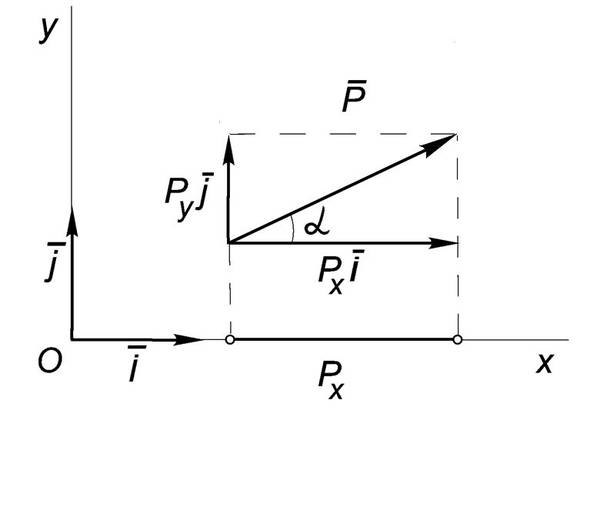
$$ P_x = X = |\vec{Р}| \cdot \cos (\vec{Р}, \vec{i}) = P \cdot \cos \alpha $$
$$ P_y = Y = |\vec{Р}| \cdot \cos (\vec{Р}, \vec{j}) = P \cdot \sin \alpha $$
, где $\vec{i}$ – единичный вектор оси /Ox/, а $\alpha$ – угол между ним и силой $\vec{Р}$ (Рис.1).
Таким образом:
$$ P_x > 0\text{, если }0 \leq \alpha < \frac{\pi}{2} $$ $$ P_x = 0\text{, если } \alpha = \frac{\pi}{2} $$ $$ P_x < 0\text{, если } \frac{\pi}{2} < \alpha \leq \pi $$
Проекция силы на ось равна нулю, если сила перпендикулярно оси.
Аналогично находится проекция силы Р на ось Oy.
Вектор $ \vec{Р} $ может быть выражен:
$$\vec{Р} = P_x \cdot \vec{i} + P_y \cdot \vec{j} = X \cdot \vec{i} + Y \cdot \vec{j}$$
А равнодействующая плоской системы двух сходящихся сил равна диагонали параллелограмма, построенного на этих силах, как на сторонах.
Модуль и направление искомого вектора силы Р можно найти по формулам:
$$ P = \sqrt{X^2 + Y^2} \\ \cos (\vec{Р}, \vec{i}) = \frac{X}{P} \\ \cos (\vec{Р}, \vec{j}) = \frac{Y}{P} $$
Момент силы относительно центра
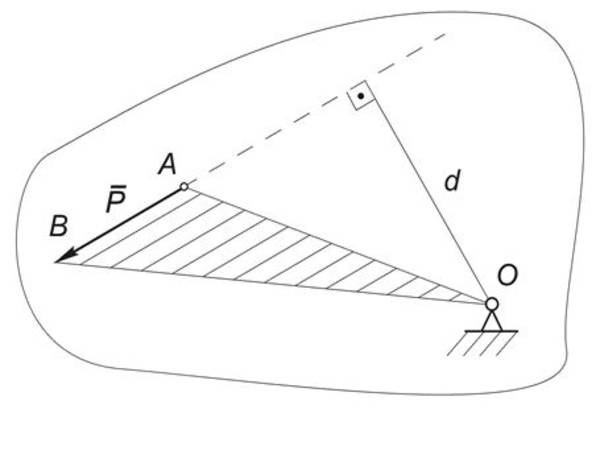
Приложим в точке А силу P и выясним - чем определяется момент силы относительно точки О, который характеризует вращательное действие этой силы относительно точки О(Рис.1).
Очевидно, что воздействие силы на тело будет зависеть не только от ее величины, но и от того, как она направлена, и в конечном итоге будет определяться ее моментом относительно центра О.
Рассмотренное определение момента силы подходит только для плоской системы сил.
Определение 1. Моментом силы Р относительно центра О называется
взятое со знаком $\pm$ произведение модуля силы на ее плечо – то есть длину
перпендикуляра, опущенного из моментной точки на линию действия силы.
Правило знаков: момент силы считается положительным, если сила
стремится повернуть тело против хода часовой стрелки и отрицательным, если
она вращает тело по ходу часовой стрелки.
В соответствии с данным определением момент силы численно равен удвоенной площади треугольника OAB, построенного на векторе силы P с вершиной в моментной точке: $M_0(P) = P\cdot d = 2S\Delta_{OAB}$ .
Отметим, что момент силы относительно точки О равен нулю, если линия действия силы проходит через моментную точку.
Уравнения равновесия плоской системы сил
Уравнения равновесия плоской системы сил,
которые можно записать в трех различных формах:
- Первая форма:
$$ \sum X=0 \\ \sum Y=0 \\ \sum M_A=0 $$ - Вторая форма:
$$ \sum M_A=0 \\ \sum M_B=0 \\ \sum Y=0 $$ , где ось Oy не перпендикулярна отрезку АВ - Третья форма:
$$ \sum M_A=0 \\ \sum M_B=0 \\ \sum M_C=0 $$ , где точки А, В и С не лежат на одной прямой.
Таким образом, любая из этих трех форм эквивалентна условию равновесия плоской системы сил и наоборот.
Центр тяжести
Центр тяжести - точка, через которую проходит равнодействующая сил тяжести при любом пространственном расположении тела.
Если тело имеет ось или центр симметрии, то центр тяжести лежит там.
Центр тяжести квадрата и прямоугольника - точка пересечения его диагоналей.
Центр тяжести круга - в его центре.
Центр тяжести треугольника - в точке пересечения медиан.