Момент силы относительно центра

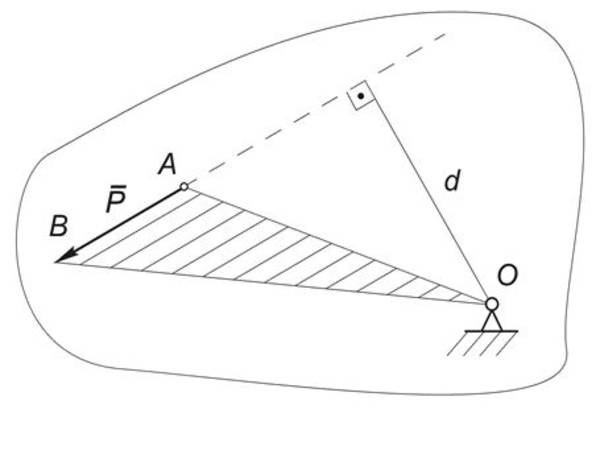
Рассмотрим тело, которое закреплено в центре О и может поворачиваться вокруг оси, проходящей через точку О и перпендикулярной к плоскости чертежа. Приложим в точке А этого тела силу P и выясним, чем определяется вращательное действие этой силы (Рис.1).

Рис.1

Очевидно, что воздействие силы на тело будет зависеть не только от ее величины, но и от того, как она направлена, и в конечном итоге будет определяться ее моментом относительно центра О.

Определение 1. Моментом силы Р относительно центра О называется взятое со знаком $\pm$ произведение модуля силы на ее плечо – то есть длину перпендикуляра, опущенного из моментной точки на линию действия силы.

Правило знаков: момент силы считается положительным, если сила стремится повернуть тело против хода часовой стрелки и отрицательным, если она вращает тело по ходу часовой стрелки.

В соответствии с данным определением момент силы численно равен удвоенной площади треугольника OAB, построенного на векторе силы P с вершиной в моментной точке: $M_0(P) = P\cdot d = 2S\Delta_{OAB}$ .

Отметим, что момент силы относительно точки О равен нулю, если линия действия силы проходит через моментную точку.

Рассмотренное определение момента силы подходит только для плоской системы сил. В общем случае для однозначного описания вращательного действия силы введем следующее определение.

Определение 2. Вектор-моментом силы Р относительно центра О называется вектор, который:

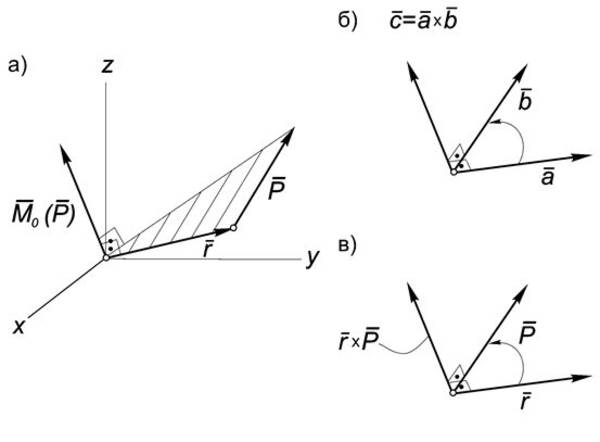
• приложен в моментной точке О перпендикулярно к плоскости треугольника, построенного на векторе силы с вершиной в моментной точке;
• направлен по правилу право винта;
• равен по модулю моменту силы Р относительно центра О (Рис.1а).

Правило правого винта, известное также из курса физики как правило буравчика, означает, что если смотреть навстречу вектор-моменту $\vec{М_0}(\vec{P})$ , мы увидим вращение силой $\vec{P}$ плоскости своего действия, происходящим против хода часовой стрелки.

Обозначим через $\vec{r}$ радиус-вектор точки приложения силы $\vec{P}$ и докажем, что справедлива следующая

Теорема 1. Вектор-момент силы $\vec{P}$ относительно центра О равен векторному произведению радиус-вектора $\vec{r}$ и вектора силы $\vec{P}$ :

$$\vec{M_0}(\vec{P}) = ( \vec{r} \times \vec{P})$$

Напомним, что векторным произведением векторов $\vec{a}\text{ и }\vec{b}$ называется вектор $\vec{c}$ , который (Рис.2б):

Рис.2

• перпендикулярен к векторам $\vec{a}\text{ и }\vec{b}$ ;
• образует с ними правую тройку векторов, то есть, направлен так, что, смотря навстречу этому вектору, мы увидим поворот от вектора $\vec{a}$ к вектору $\vec{b}$ на наименьший угол происходящим против хода часовой стрелки;
• равен по модулю удвоенной площади треугольника, построенного на этих векторах:

$$|\vec{c}| = |\vec{a} \times \vec{b}| = |\vec{a}|\cdot|\vec{b}|\cdot\sin(\vec{a},\,\vec{b})$$

Для доказательства теоремы отметим, во-первых, что вектор, равный векторному произведению векторов $\vec{r}\text{ и }\vec{P}$ будет коллинеарным вектору $\vec{M_0}(\vec{P})$.

Чтобы убедиться в этом, достаточно отложить эти векторы от одной точки (Рис.1в). Итак, $(\vec{r} \times \vec{P}) \uparrow \uparrow \vec{M_0}(\vec{P})$.

Во-вторых, модуль векторного произведения этих векторов будет равен:

$$|\vec{r} \times \vec{P}| = |\vec{r}|\cdot|\vec{P}|\cdot\sin(\vec{r},\,\vec{P}) = P \cdot d =|\vec{M_0}(\vec{P})|$$

, откуда и следует соотношение теоремы.

Следствием этой теоремы является:

Теорема Вариньона (о моменте равнодействующей сходящихся сил). Вектор- момент равнодействующей системы сходящихся сил относительно произвольного центра О равен геометрической сумме вектор-моментов всех сил системы относительно этого центра:

$$\vec{M_0}(\vec{R}) = \sum_{i=1}^{i=n}\vec{M_{0\,\,i}}(\vec{P_i})$$

В самом деле, момент равнодействующей, с учетом теоремы 1 и аналитического определения равнодействующей сходящихся сил, будет равен:

$$ \vec{M_0}(\vec{R})= \vec{R}\times\vec{r} \,\,\,\;\;\text{ , т.к. } \vec{M_0}(\vec{P}) = ( \vec{r} \times \vec{P}) \\ \vec{R}\times\vec{r}= \vec{r}\times\sum_{i=1}^{i=n}\vec{P_i} \,\,\,\;\;\text{ , т.к. } (\vec{P_1}, \vec{P_2}, \dots, \vec{P_n}) \sim \vec{R} = \sum_{i=1}^{i=n} \vec{P_i} \\ \vec{r}\times\sum_{i=1}^{i=n}\vec{P_i} = \sum_{i=1}^{i=n}(\vec{r}\times\vec{P_i}) = \sum_{i=1}^{i=n}\vec{M_{0\,\,i}}(\vec{P_i}) $$

Для плоской системы сходящихся сил геометрическая сумма в теореме Вариньона переходит в алгебраическую:

$$M_0(R)=\sum_{i=1}^{i=n}M_{0\,\,i}(\vec{P_i})$$

• В учебной литературе термин «момент» применяют для обозначения как момента силы, так и ее вектор-момента.