Одной из основных задач, решаемых статикой, является замена одной системы сил другой – эквивалентной ей.

Такая процедура позволяет все многообразие систем сил свести к простейшим каноническим системам, классифицировать их и получить уравнения равновесия, необходимые для решения практических задач.

Ключевую роль в проведении таких преобразований систем сил играет следующая теорема.

Лемма Пуансо

Мы уже выяснили, что силу, приложенную к ТТ, можно переносить вдоль линии ее действия. Сейчас мы увидим, что при определенных условиях эту силу можно переносить даже параллельно своему первоначальному положению.

Лемма Пуансо. Действие силы Р, приложенной к ТТ не изменится, если эту силу перенести в любую точку О этого тела – центр приведения, добавив пару сил с моментом, равным моменту силы Р относительно центра приведения.

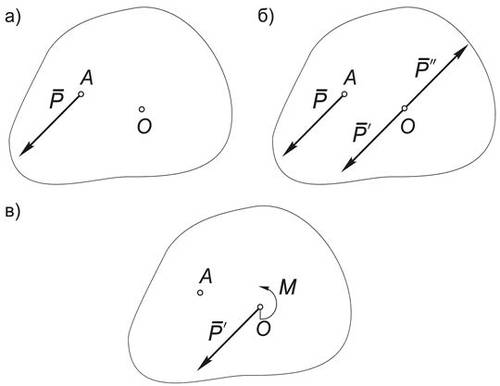
Для доказательства рассмотрим силу Р, приложенную к телу в точке А (Рис.1а).

Для доказательства рассмотрим силу Р, приложенную к телу в точке А

Рис.1

Согласно аксиоме 3 действие силы $\vec{P}$ на ТТ не изменится, если к ней добавить уравновешенную систему сил: $(\vec{P'}, \vec{P''}) \sim 0$.

Выберем силы этой уравновешенной системы так, чтобы они были равны по модулю и параллельны силе $\vec{P}$ (Рис.1б) :

$$\vec{P'}=\vec{P}=-\vec{P''}$$

Тогда полученную систему трех сил можно трактовать как силу $\vec{P'}$ , приложенную в центре О, и пару сил $(\vec{P}, \vec{P''})$ с моментом $М(\vec{P}, \vec{P''}) = М_О (\vec{P})$ :

$$\vec{P} \sim (\vec{P}, (\vec{P'}, \vec{P''})) \sim (\vec{P'}, (\vec{P}, \vec{P''}))$$

Лемма доказана.

Сила $\vec{P'}$, приложенная в точке О, называется приведенной, а пара $(\vec{P}, \vec{P''})$ – присоединенной.

Напомним, что пару $(\vec{P}, \vec{P''})$ можно заменить моментом $\vec{M}$ , величина которого равна моменту силы $\vec{P}$ относительно центра приведения О (Рис.1в), поэтому:

$$\vec{P} \sim (\vec{P'} , (\vec{P}, \vec{P''})) \sim (\vec{P'}, \vec{M})$$