Перпендикулярность прямых и плоскостей
Прямые
Перпендикулярные прямые в пространстве – две пересекающиеся или скрещивающиеся прямые, угол между которыми равен 90º.
Прямая и плоскость
Признак перпендикулярности прямой и плоскости:
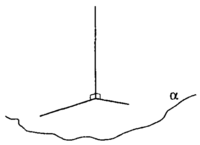
Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна этой плоскости. См.Рис.1.
Перпендикулярные прямые обозначаются: a⊥b.
Лемма о перпендикулярности двух прямых к третьей прямой. Если одна из двух параллельных прямых перпендикулярна к третьей прямой, то и другая прямая перпендикулярна к этой прямой.
Прямая перпендикулярна к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости.
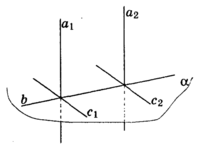
Свойства прямых, перпендикулярных плоскости: См.Рис.2.
- Если плоскость перпендикулярна одной из параллельных прямых, то она перпендикулярна и другой.
- Если одна из двух параллельных прямых перпендикулярна плоскости, то и другая прямая перпендикулярна этой плоскости.
- Если две прямые перпендикулярны одной и той же плоскости, то они параллельны.
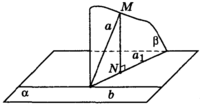
Теорема о трех перпендикулярах. Наклонная к плоскости перпендикулярна к прямой, лежащей в этой плоскости, тогда и только тогда, когда проекция наклонной перпендикулярна этой прямой.
См.Рис.3.
Теорема, обратная теореме о трех перпендикулярах. Прямая, проведённая в плоскости через основание наклонной перпендикулярно к ней, перпендикулярна и к её проекции.
Плоскости
Признак перпендикулярности двух плоскостей:
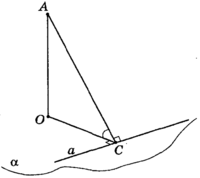
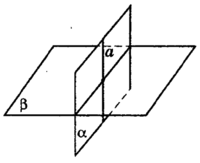
Если одна из двух плоскостей содержит прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны. См.Рис.4.
Рекомендуем
| ← Скрещивающиеся прямые | Стереометрия ( Справочник ) | Углы в пространстве → |
| Рекомендуем для обучения: | ||
|---|---|---|
| Геометрия ( Справочник ) | ||