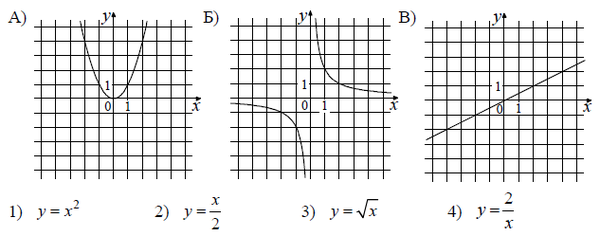Функции, их свойства

Функция - это такая зависимость переменной у от переменной х, при которой каждому значению переменной х соответствует единственное значение переменной у.

Переменная х называется независимой переменной или аргументом.

Переменная у называется зависимой переменной и говорят, что переменная у является функцией от переменной х.

Область определения функции - это все значения независимой переменной.

Область значений функции - это все значения, которые принимает зависимая переменная.

График функции - это множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции.

Нули функции - это значения аргумента, при которых функция обращается в нуль.

Функция называется возрастающей на некотором промежутке I, если для любых $x_1,\,,x_2 \in I$ таких, что $x_1<x_2$ верно неравенство $f(x_1)<f(x_2)$.

Функция называется убывающей на некотором промежутке I, если для любых $x_1,\,,x_2 \in I$ таких, что $x_1<x_2$ верно неравенство $f(x_1)>f(x_2)$.

---

Пример 1 Установите соответствие между графиками функций и формулами, которые их задают.

Видео-решение.